深圳国际研究生院戚铭尧合作在竞争性设施选址问题的理论方法研究上取得新进展

竞争性设施选址问题(Competitive Facility Location Problem, CFLP)是指在多个市场主体之间为了赢得同类产品或服务的市场份额而开展的一种博弈决策问题，它有着广泛的应用基础，例如零售店、购物中心、停车场、租车店、电动车充电站的选址等。其中，序贯(Sequential)竞争性设施选址问题(S-CFLP)考虑一种更加复杂的决策环境，即市场中的主导方(leader)在进行自己的选址决策时，还必须预计跟随方(follower)在得知主导方决策后所做出的最优反制决策，从而使主导方得到具有预见效果的最优决策，属于一种斯坦伯格博弈问题。常规的CFLP问题可以建模为一个单层的混合整数线性规划(MILP)，或者混合整数凹优化模型，求解相对容易，而S-CFLP问题则是一个上下两层均为混合整数非线性规划(MINLP)的双层规划问题，其求解难度极大，除了暴力枚举法之外，目前尚没有能求解这一问题的精确算法。

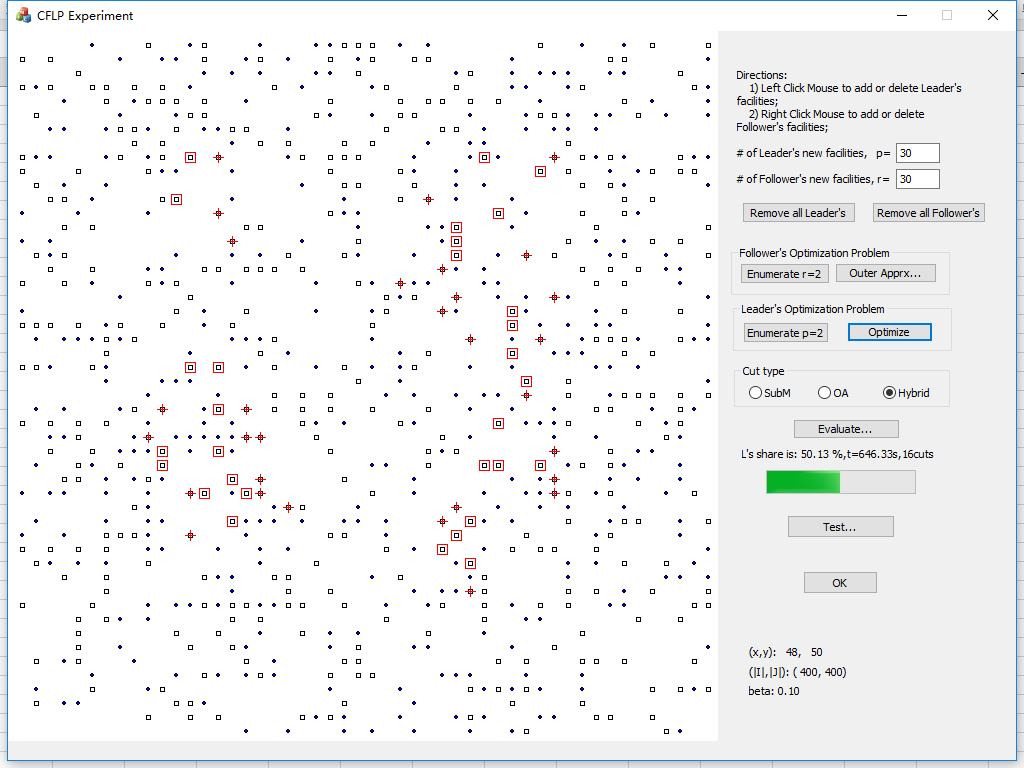
图1. 序贯竞争性设施选址问题求解界面(圆点为顾客点，黑色方框为候选设施点，红色方块为领导者所选的设施，红十字为跟随者选择的设施)

针对这一复杂的优化问题，清华大学深圳国际研究生院戚铭尧副教授与美国密歇根大学安娜堡分校江瑞威副教授和沈思倩副教授合作，提出了一种高效的精确算法。首先，将原始的双层优化问题通过巧妙的数学变换，等价转化为一种单层混合整数非线性规划模型(MINLP)。其次，为了处理棘手的混合整数非线性约束，该研究推导出了两类有效不等式(线性约束)来代替非线性约束：一类是将领导者的市场份额函数转化为一个集合函数，并证明该函数具有次模性(Submodularity)，从而推导出一种次模割(Submodular Cut);另一类是利用决策变量是0-1变量的特点，将原本非凸非凹的市场份额函数放大为一个凹函数，同时保持整数解上的值不变，从而在整数解上生成外逼近割(Outer Approximation Cut)。通过生成这两种割，使得问题的求解速度提高了至少两个数量级。此外，由于生成有效不等式(割)需要求解出下层问题，该研究进一步提出了一种可以在多项式时间内求解下层问题的近似算法，使得算法速度再次提高2-3倍。最后，该研究还提出了一种近似求解模型，能把原问题转化为一个具有精度保证的混合整数二阶锥规划(MISOCP)问题，从而可以直接用已有的求解器来求解。

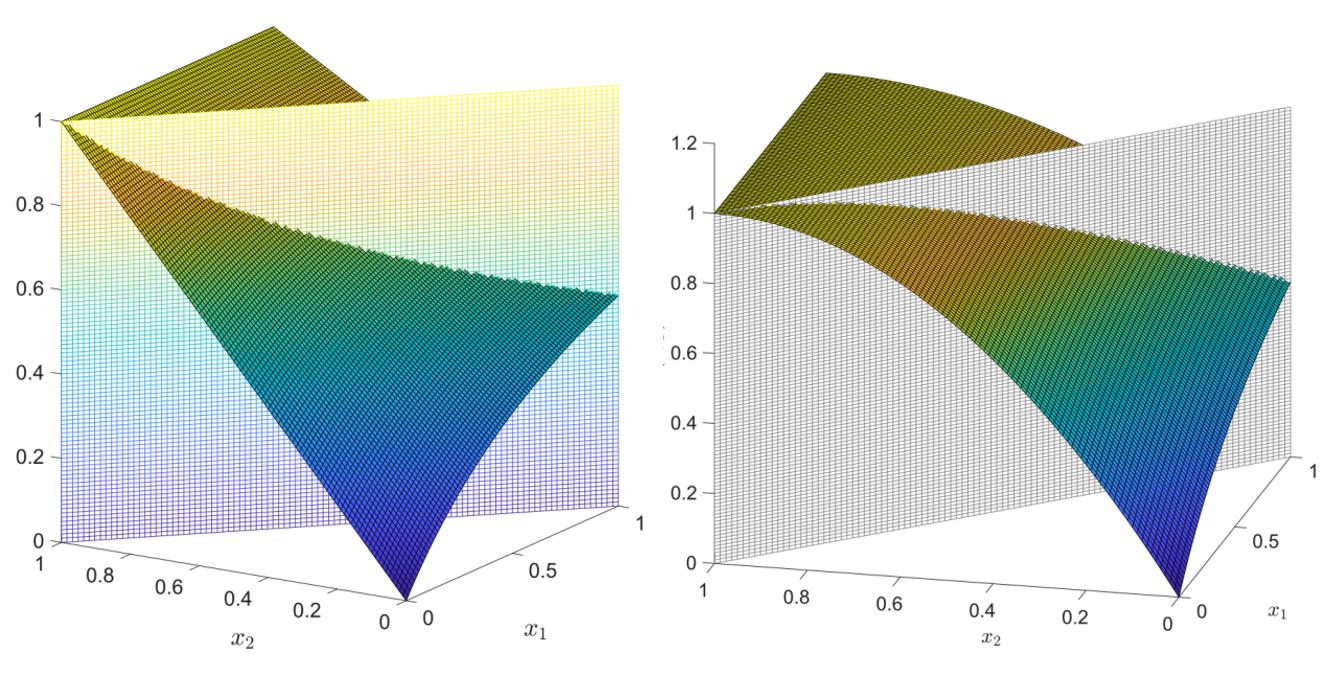
图2. 原始市场份额函数(左)和凹化后的市场份额函数(右)，见曲面和平面的交线

数值实验表明，基于等价模型及其算法，可以求得最优解的问题规模达到100个候选设施、2000个顾客点，这个规模对于精确算法来说已经足够大，甚至远高于已有的启发式算法所能求解的规模。数值实验还表明，算法只需要用最初的几次迭代(数秒内)，即可得到离最优解非常接近的近似解(gap<3%)，这表明算法还可以为实际应用中可能出现的更大规模的问题提供高质量的近似解。利用所提出的理论方法，该研究还探讨了用户选择模型的参数取值对选址行为的影响。研究发现，反映空间阻隔效应的参数越小，领导者和跟随者的设施选址都宜尽量靠近市场区域中心，而当空间阻隔效应较大时，二者的设施宜在区域内相对分散。该研究还对问题假设进行了多方面的拓展，使得所提出的方法还可以适用于更多的场景，例如：同时决策设施的规模、考虑更多的市场竞争者、市场聚集效应等。

该研究工作以“序贯竞争性设施选址：精确与近似算法”(Sequential Competitive Facility Location: Exact and Approximate Algorithms)为题，发表在国际学术期刊《运筹学》(Operations Research)上。清华大学深圳国际研究生院戚铭尧副教授为文章的第一作者，美国密歇根大学安娜堡分校江瑞威副教授为第二作者，该校沈思倩副教授为第三作者兼通讯作者。该工作得到国家自然科学基金面上项目资助。

【免责申明】本专题图片均来源于学校官网或互联网，若有侵权请联系400-0815-589删除。